Basic statistics

Measure of central tendency

• Mean
• Median
• Mode

Population and Sample

• If all information required is in hand then population is used

• Sample is a subset of population
• Sample is used to reduce cost or when it is not possible to get all the population information.

Mean

• Sample and population mean is same.

\[Mean = \frac{sum of all observation}{ number of observations}\]

Median

• Middle value of sorted data

Mode

• Observation that occurs most frequently

Measure of Dispertion

Standard devaitions or variants

• Variance is difference between population and sample

Random variables and Probability Distributions

• Random variable is a quantity whose possible values depends, in some clearly-defined way, on a set of random events.

• A probability distribution is essentially a theoritical model depicting the possible values a random variable may assume along with probability of occurance

Normal distribution

• Normal(mean, standard_deviation)
• When mean 0, standard deviation 1 then standard normal distribution

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
x_axis = np.arange(-4, 4. 0.1)
plt.plot(x_axis, norm.pdf(x_axis, 0, 1))
plt.show()

T distribution

• Students t-distribution
• Normal distribution describes the mean of population where the T-distribution describes the mean of the sample drawn from a population.
• The T-distribution for each sample could be different.

• When sample size is big, then T-disribution resemble the normal distribution.

• When Degree of freedom increases then t distribution turns into Normal distribution

• Assumptions required for t distribution

  1. Scale of measurement –> follows continuous or ordinal scale.
  2. Simple random sample –> representative randomly selected of a population.
  3. Bell shaped distribution –> when plotted follow normal distribution.
  4. Homogeneity of variance-> test required to test this. To avoid the test statistics to be biased against the larger sample sizes.

Probability of getting a high or low teaching evolution.

import scipy.stats
prob = scipy.stats.norm.cdf((
    (X- mean) / std
))
prob_greater_than = 1- prob

When to test t-test or Z-test

• When population’s standard deviation is known then Z-test otherwise t-test

• 4 Scenarios

  1. We are comparing sample mean to a population mean and standard deviation of population is known then Z test.
  2. We are comparing sample mean to a population mean and standard deviation of population is not known then T test.
  3. Comparing means of two independent samples with unequal variance. Always use T Test.
  4. Comparing means of two independent samples with equal variance. Always use T Test.

* Z test normal distribution and t-test T distribution.

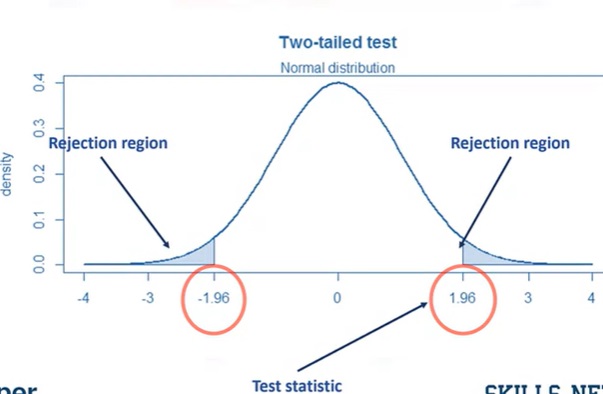
Dealing with tails and rejection

Equal vs Unequal Variances

• A t-test called Leven’s Test to assess the equality of variances
• Null hypothes Ho: Population variances are equal
• If p < 0.05 reject null hypothesis

scipy.stats.levene(
    first_var,
    second_var,
    center='mean'
)

• In case of p_value 0.05 e.g. we have a p_value = 0.66 we can say the variances are equal.
• So where it will be used. When we will run t-test we set the option, equal_var = True

scipy.stats.ttest_ind(
    first_var,
    second_var,
    equal_var=True
)

ANOVA

• when comparison is done between more than two groups then ANOVA is used
• F distribution is used
• Null hypothesis is mean are same
• We fail to reject null hypothesis if the p value F test > 0.05 and means same mean

# Three variables are
# forty_lower, forty_fifty_seven, fiftyseven_older
f_statistics, p_value = scipy.stats.f_oneway(
    forty_lower,
    forty_fifty_seven,
    fiftyseven_older
)
print(f'F statistics = {f_statistics}\n and P value is = {p_value}')

Correlation

• Categorical variable

  • Chi-square Test

    • But start with a cross tab
• Null hypothesis Ho: No relation
• Alternative hypothesis H1: they are related

scipy.stats.chi2_contingency(
    cont_table,
    correction=False
)
# first value = chi_squaure test value
# second value is p value
# Degree of freedom third value
# last array expected values

• Continuous Variable

  • pearson Correlation

    • But start with a scatter plot
• Null hypothesis Ho: No relation
• Alternative hypothesis H1: they are related

pearson_value, p_value = scipy.stats.pearsonr(
                         first_variable
                         second_variable
                         )

Regression in place of T-test

scipy.stats.ttest_ind(
    first_var,
    second_var,
    equal_var=True
)

import statsmodel.api as sm
X = first_var
y = second_var
X =  sm.add_constant(X)
model = sm.OLS(y, X).fit()
predictions = model.predict(X)
model.summary()

Regression in place of ANOVA

import statsmodel.api as sm
from statsmodel.formula.api import ols
lm = ols('beauty ~ age_group' data = ratings_df).fit()
table = sm.stats.anova_lm(lm)
print(table)

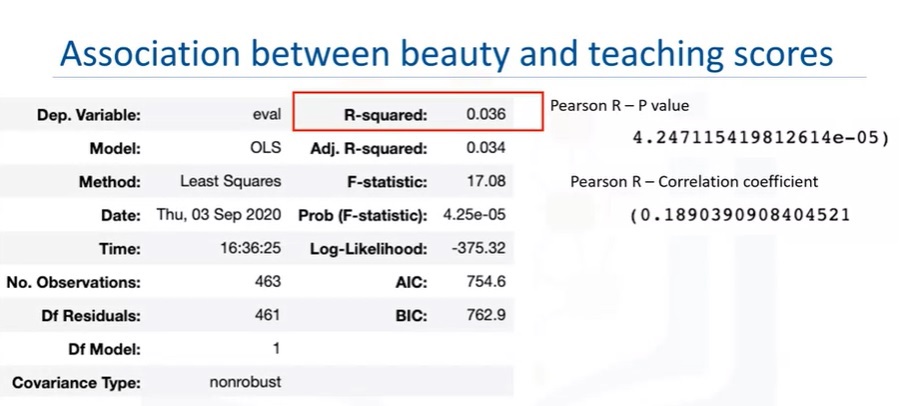
Regression in place in Correlation

import statsmodel.api as sm
X = first_var
y = second_var
X =  sm.add_constant(X)
model = sm.OLS(y, X).fit()
predictions = model.predict(X)
model.summary()